ESPACIO VECTORIAL.

Un espacio vectorial es una estructura algebraica creada a partir de un conjunto no vacío, una operación interna (llamada suma, definida para los elementos del conjunto) y una operación externa (llamada producto por un escalar, definida entre dicho conjunto y otro conjunto, con estructura de cuerpo ).

A los elementos de un espacio vectorial se les llama vectores y a los elementos del cuerpo, escalares.

Propiedades: sea V un conjunto no vacío. Supongamos que en V hay definida una operación suma, que denotaremos por +, y una operación producto por un escalar, que denotaremos por ·. Diremos que (V, +, ·) es un espacio vectorial real (o simplemente un espacio vectorial) si se verifican las siguientes propiedades: 

1. Propiedad asociativa (+): (u + v) + w = u + (v + w), ∀ u, v, w ∈ V . 

2. Propiedad conmutativa: u + v = v + u, ∀ u, v, ∈ V . 

3. Existencia de elemento neutro: ∃ 0 ∈ V | 0 + v = v, ∀ v ∈ V .

4. Existencia de elemento opuesto: ∀ v ∈ V ∃ -v ∈ V | v + (-v) = 0. 

5. Propiedad distributiva I: a · (u + v) = a · u + a · v, ∀ a ∈ R, ∀ u, v ∈ V .

 6. Propiedad distributiva II: (a + b) · v = a · v + b · v, ∀ a, b ∈ R, ∀ v ∈ V . 

7. Propiedad asociativa (·): a · (b · v) = (ab) · v, ∀ a, b ∈ R, ∀ v ∈ V .

 8. Elemento unidad: 1 · v = v, ∀ v ∈ V . 

Los elementos de V suelen denominarse vectores y los números reales como escalares . 

Un espacio vectorial sobre un cuerpo  (como el cuerpo de los números reales o los números complejos) es un conjunto  no vacío, dotado de dos operaciones para las cuales será cerrado:

operación interna tal que:

1) tenga la propiedad conmutativa, es decir

2) tenga la propiedad asociativa, es decir

3) tenga elemento neutro 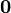, es decir

  

4) tenga elemento opuesto, es decir

 

y la operación producto por un escalar:

operación externa tal que:

5) tenga la propiedad asociativa:

  

6)  sea elemento neutro del producto:

 

7) tenga la propiedad distributiva del producto respecto la suma de vectores:

  

8) tenga la propiedad distributiva del producto respecto la suma de escalares:

  

Espacio vectorial: https://www.youtube.com/watch?v=L9K2YzLlNYQ

Subespacio vectorial: en álgebra lineal, un subespacio vectorial es el subconjunto de un espacio vectorial, que satisface por sí mismo la definición de espacio vectorial con las mismas operaciones que V.

Sea  un espacio vectorial sobre  y 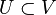 no vacío,  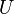es un subespacio vectorial de  si:

Un subespacio vectorial que cumple las dos condiciones anteriores es un espacio vectorial.

Dado 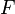 un subespacio vectorial, se tiene:

Para i) el abuso de lenguaje , e incluso  es correcto.

Para ii) el abuso de lenguaje , e incluso  es correcto.

Es posible sintetizar i) y ii) en una condición única:

Si V es un espacio vectorial, entonces un subconjunto no vacío U de V es un subespacio vectorial si y sólo si para cualesquiera dos vectores v, w pertenecientes a U y cualesquiera escalares r y s pertenecientes al cuerpo asociado, el vector  es también un elemento de U.

Subespacio vectorial:  https://www.youtube.com/watch?v=H_hGlOBnoaA

Combinación lineal y generación  de un espacio: dados los vectores  de un espacio vectorial , llamamos combinación lineal de  a cualquier vector de la forma: , donde  (i.e. son escalares, por ejemplo, en ). Lamamos espacio generado por  al conjunto:

Lo anterior se generaliza de forma natural a  vectores.

Ejemplo: Si  y , ambos considerados como vectores en , y  , entonces tenemos que es una combinación lineal de dichos vectores y que

Note que dicho espacio generado es menor al espacio . Por ejemplo .

En particular, la combinación lineal de un sistema de vectores se trata de un vector de la forma

con los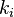  elementos de un cuerpo.Como la suma vectorial de los múltiplos de cada vector del sistema.

                                            

                           Combinación lineal de dos vectores en el espacio.

Combinación lineal  y generación  del espacio: https://www.youtube.com/watch?v=R31v8HrvsnA

Dependencia e independencia lineal: en álgebra lineal, un conjunto de vectores es linealmente independiente si ninguno de sus vectores componentes puede ser escrito con una combinación lineal de los restantes. Por ejemplo, en R³, el conjunto de vectores (1, 0, 0), (0, 1, 0) y (0, 0, 1) es linealmente independiente, mientras que (2, −1, 1), (1, 0, 1) y (3, −1, 2) no lo es, ya que el tercero es la suma de los dos primeros.

Dado un conjunto finito de vectores , se dice que estos vectores son linealmente independientes si existen números , donde la ecuación

se satisface únicamente cuando  son todos cero. En caso contrario, se dice que son linealmente dependientes.

Nótese que el símbolo a la derecha del signo igual no es cero, sino que simboliza al vector nulo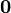 . El conjunto de vectores nulos forma la matriz nula. Si tales números no existen, entonces los vectores son linealmente independientes. La definición anterior también puede extenderse a un conjunto infinito de vectores, concretamente un conjunto cualquiera de vectores es linealmente dependiente si contiene un conjunto finito que sea linealmente dependiente.

Utilizando conceptos de espacios vectoriales podemos redefinir la independencia lineal así:

Un conjunto de vectores  de un espacio vectorial es linealmente independiente si 

Esta idea es importante porque los conjuntos de vectores que son linealmente independientes, generan un espacio vectorial y forman una base para dicho espacio. Entre las propiedades de los vectores linealmente dependientes e independientes encontramos:

1. Un conjunto de vectores es linealmente dependiente si y solamente si alguno de los vectores es combinación lineal de los demás.
2. Si un conjunto de vectores es linealmente independiente cualquier subconjunto suyo también lo es. Obviamente, si tenemos un conjunto de vectores tales que ninguno de ellos es combinación de los demás, escogiendo solamente unos cuantos, no podrán ser combinación de los otros.
3. Si un conjunto de vectores es linealmente dependiente, también lo es todo conjunto que lo contenga.
4. Un conjunto de vectores son linealmente dependientes si y sólo si son paralelos.
5. Un conjunto de vectores son linealmente dependientes si los componentes entre ellos son proporcionales, bien sea directa o inversamente proporcional. Ya que un conjunto de vectores es linealmente dependiente si y solo si tiene algún vector que es combinación lineal de los demás, si metemos este conjunto de vectores en otro más grande, seguimos teniendo el vector que es combinación lineal de otros, por tanto, el conjunto más grande será linealmente dependiente.

Combinación lineal ; dependencia e independencia lineal: https://www.youtube.com/watch?v=hEwMcCd-57o

Bases :Se llama base de un espacio (o subespacio) vectorial a un sistema generador de dicho espacio o subespacio, que sea a la vez linealmente independiente.

Propiedades de las bases.

 1. Una base de S es un sistema generador minimal de S (lo más pequeño posible).

 2. Además es un conjunto independiente maximal dentro de S (lo más grande posible).

 3. Una base de S permite expresar todos los vectores de S como combinación lineal de ella, de manera única para cada vector. 

Ejemplo de base:

 1. La base canónica (o base natural, o base estándar) de ℜ n: e1 = (1,0,. . . ,0) e2 = (0,1,. . . ,0) ........ en = (0,0,. . . ,1) 

- Son linealmente independientes porque forman un determinante no nulo. 

- Son sistema generador de ℜ n porque todo vector (a1,a2,. . . ,an)∈ ℜ n se puede expresar como combinación lineal de ellos: (a1,a2,. . . ,an)= a1(1,0,. . . ,0)+ a2(0,1,. . . ,0)+ . . . + an(0,0,. . . ,1) 

Dimensión:Todas las bases de un mismo espacio o subespacio tienen el mismo número de vectores. Se llama dimensión de dicho espacio o subespacio. 

Propiedades de la dimensión.

 1. Significado físico de la dimensión: el espacio tiene dimensión 3, los planos dimensión 2, las rectas dimensión 1, el punto dimensión 0. El subespacio {0} es el único de dimensión 0. 2. La dimensión de un subespacio en ℜn , coincide con el número de parámetros libres en su forma paramétrica. (1 parámetro=recta, 2 parámetros= plano...) 

3. Si S y T son subespacios y S está contenido en T, entonces dim S ≤ dim T. Además, si se da la igualdad, dim S = dim T, entonces ambos espacios han de coincidir. 

4. El rango de una familia de vectores, es igual a la dimensión del subespacio que generan. Es decir: si v1,v2,. . . vn generan un cierto subespacio S, y si el rango de dicho conjunto es r, entonces dim S = r. (Si un cierto conjunto de vectores tienen rango 2, entonces generan un plano; etc.) 

Ejemplos de dimensión:

 1. ℜn tiene dimensión n, pues tiene una base de n elementos (p.ej. la canónica). 

2. P2= {polinomios de grado≤ 2 con coeficientes reales} tiene dimensión

 3. Una base de P2 es, por ejemplo, la formada por los tres polinomios siguientes: 1+0x+0x2 , 0+x+0x2 , 0+0x+x2 (es decir, los polinomios 1, x, x2 ). Otra base: 1+2x+3x2 , 4+x2 , 3–x–5x2 . 

Base y dimensión , ejercicio:https://www.youtube.com/watch?v=P_gPauR3j8M

Rango, Nulidad, Espacio de los Renglones y Espacio de las Columnas de una matriz:                                                                                                         Definición: espacio nulo y nulidad de una matriz N_A se denomina el espacio nulo de A y V(A) = dim N_A se denomina nulidad de A.

Si N_A contiene solo al vector cero, entonces V(A) = 0

Sea una matriz de m x n entonces la imagen de A, denotada por Im(A), está dada por Im(A) = { Y ϵ R^m : AX = Y para alguna X ϵ R^m }

Teorema: sea A una matriz de m x n entonces la imagen de A Im(A) es un subespacio de R^m

Definición: rango de una matriz

Sea A una matriz de m x n entonces el rango de A, denotado por P(A) está dado por P(A) = dim Im(A)

Definición: espacio de los renglones y espacio de las columnas de una matriz

Si A es una matriz de m x n, sean { r₁, r₂, …, r_m} los renglones de A y { c₁, c₂, …, c_n} las columnas de A. entonces se define:

RA = espacio de los renglones de A= gen{ r₁, r₂, …, r_m}

Y

CA = espacio de las columnas de A = gen { c₁, c₂, …, c_n}

Ejemplo:

^{Rango y nulidad: https://www.youtube.com/watch?v=RoKpDwT5Lxk}

 Cambio de base: En un espacio vectorial V, dadas dos bases B y B’ , se llama matriz de cambio de base (o de cambio de coordenadas) de B a B’ a la matriz que contiene en sus columnas las coordenadas de los vectores de la base B expresados en función de la base B’. Su utilidad es la siguiente: Conocidas las coordenadas de un vector en base B, nos permitirá hallar las coordenadas de dicho vector en base B’. En efecto, sean (a1, a2, . . . an) las coordenadas de un vector en base B, y sea P la matriz de cambio de base de B a B’. 

Ejemplo.

 Consideremos en ℜ2 las dos bases siguientes: la base del ejemplo (1) anterior, B ={ (2,3), (1, –1) } la base canónica B’ ={ (1,0), (0,1) } • Vamos a construir la matriz de cambio de base de B a B’. Para ello debemos expresar los vectores de la base B en función de la base canónica B’. (2,3) = 2·(1,0) + 3·(0,1) Æ coordenadas (2,3) (–1,1)= 1·(1,0) –1·(0,1) Æ coordenadas (1, –1) Introduciendo estas coordenadas en las columnas de una matriz, tendremos la matriz de cambio de base de B a B’: P= 2 1

                                                                                      3 -1

Matriz de cambio de base: https://www.youtube.com/watch?v=wGl-E5LRvac

Bases ortonormales y proyecciones:

Definición: una proyección P ∈ C n×n es ortogonal si Ker(P) = (Im(P))⊥.

Proposicion: una proyección P es ortogonal si y s´olo si P = P ∗ (i.e., es hermıtica). 

Proposicion: una matriz P ∈ C n×n de rango r es una proyecci´on ortogonal si y solo si existe una matriz Q ∈ C n×r , con columnas ortonormales, tal que P = QQ∗ .

Propiedades de las proyecciones ortogonales 

1 QQ∗ proyecta ortogonalmente sobre Im(Q) (paralelamente a (Im(Q))⊥ = Ker(Q∗ )). 

2 In − QQ∗ proyecta ortogonalmente sobre (Im(Q))⊥ (paralelamente a Im(Q)). 

3 Las proyecciones ortogonales de rango 1 son de la forma: Pq = qq∗ , q un vector unitario. Proyectan ortogonalmente sobre < q >. Su complementaria, In − qq∗ , es de rango n − 1 y proyecta ortogonalmente sobre < q >⊥.

Definición: una matriz P ∈ C n×n se dice que es una proyección si es una matriz idempotente. Es decir, si P2 = P. 

Proposicion: si P ∈ C n×n es una proyección tambien lo es In − P. A ´esta se le llama proyección complementaria de P y cumple que Ker(P) = Im(In − P) y Ker(In − P) = Im P.

Proposicion: si P ∈ C n×n es una proyección´ entonces Im(P) ⊕ Ker(P) = Cn

 Conclusion: si P es una proyección, proyecta C n sobre Im(P) a lo largo de Ker(P).

Proyecciones con bases ortonormales:https://www.youtube.com/watch?v=DzlfEF3yZxY