Álgebra lineal

VALORES CARACTERÍSTICOS, VECTORES

CARACTERÍSTICOS Y FORMAS CANÓNICAS

Las transformaciones lineales del espacio —como la rotación, la reflexión, el ensanchamiento, o cualquier combinación de las anteriores; en esta lista podrían incluirse otras transformaciones— pueden interpretarse mediante el efecto que producen en los vectores. Los vectores pueden visualizarse como flechas de una cierta longitud apuntando en una dirección y sentido determinados.

Los vectores propios de las transformaciones lineales son vectores que, o no se ven afectados por la transformación o se ven multiplicados por un escalar, y por tanto no varían su dirección.¹
El valor propio de un vector propio es el factor de escala por el que ha sido multiplicado.
Un espacio propio es un espacio formado por todos los vectores propios del mismo valor propio, además del vector nulo, que no es un vector propio.
La multiplicidad geométrica de un valor propio es la dimensión del espacio propio asociado.
El espectro de una transformación en espacios vectoriales finitos es el conjunto de todos sus valores propios.

Valores y vectores propios: el cálculo de los valores propios y de los vectores propios de una matriz simétrica tiene gran importancia en las matemáticas y en la ingeniería, entre los que cabe destacar, el problema de la diagonalización de una matriz, el cálculo de los momentos de inercia y de los ejes principales de inercia de un sólido rígido, o de las frecuencias propias de oscilación de un sistema oscilante.

Se denominan valores propios o raíces características de una matriz cuadrada A, a los valores de λ tales que.

\det (A - λ E) = | \begin{matrix} a_{11} - λ & a_{12} & ... a_{1 n} \\ a_{21} & a_{22} - λ & ... a_{2 n} \\ ... & ... & ... \\ a_{n 1} & a_{n 2} & a_{nn} - λ \end{matrix} | = 0

Desarrollando el determinante tenemos un polinomio de grado n en λ. Trataremos de encontrar los coeficientes del polinomio y luego, aplicaremos un método de hallar las raíces del polinomio.

Una vez hallados los valores propios, para hallar el vector propio X correspondiente al valor propio λ es necesario resolver el sistema homogéneo

A X = λ X

donde el vector X es

X = {x_{1}, x_{2,} ... x_{n}}

Siempre podemos tomar x₁ como 1, y hallar las otras n-1 incógnitas. De las n ecuaciones podemos tomar n-1, y resolver el sistema lineal.

\begin{array}{l} (a_{22} - λ) x_{2} + a_{23} x_{3} + .... + a_{2 n} x_{n} = - a_{21} \\ a_{32} x_{2} + (a_{33} - λ) x_{3} + .... + a_{3 n} x_{n} = - a_{31} \\ ............................................... \\ a_{n 2} x_{2} + a_{n 3} x_{3} + .... + (a_{n n} - λ) x_{n} = - a_{n 1} \end{array}

Formalmente, se definen los vectores propios y valores propios de la siguiente manera: Sea A: V → V es un operador lineal en un cierto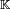

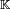\scriptstyle \mathbb{K}

-espacio vectorial V y v vector no nulo en V. Si existe un escalar no nulo c tal que

$\mathbf{A} \mathbf{v} = c \mathbf{v},\qquad \mathbf{v}\ne \mathbf{0}, c \in \mathbb{K},$

entonces decimos que v es un vector propio del operador A, y su valor propio asociado es c. Observe que si v es un vector propio con el valor propio c entonces cualquier múltiplo diferente de cero de v es también un vector propio con el valor propio c. De hecho, todos los vectores propios con el valor propio asociado c junto con 0, forman un subespacio de V, el espacio propio para el valor propio c. Observe además que un espacio propio Z es un subespacio invariante de A, es decir dado w un vector en Z, el vector Aw también pertenece a Z.

Vectores propios: conocidos los valores propios de una matriz simétrica A, se pueden calcular el vector propio X correspondiente a cada valor propio λ.

AX=λX

mediante el siguiente procedimiento. Supongamos una matriz simétrica A de dimensión 4.

\begin{array}{l} [\begin{matrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44} \end{matrix}] [\begin{matrix} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \end{matrix}] = λ [\begin{matrix} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \end{matrix}] \\ [\begin{matrix} a_{11} - λ & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} - λ & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} - λ & a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44} - λ \end{matrix}] [\begin{matrix} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \end{matrix}] = 0 \end{array}

Conocido el valor propio λ, tenemos un sistema de ecuaciones homogéneo de 4 ecuaciones con 4 incógnitas. Le damos a x₁ el valor arbitrario de 1 y lo convertimos en el sistema de tres ecuaciones con tres incógnitas

\begin{array}{l} {\begin{cases} a_{21} x_{1} + (a_{22} - λ) x_{2} + a_{23} x_{3} + a_{24} x_{4} = 0 \\ a_{31} x_{1} + a_{32} x_{2} + (a_{33} - λ) x_{3} + a_{34} x_{4} = 0 \\ a_{41} x_{1} + a_{42} x_{2} + a_{43} x_{3} + (a_{44} - λ) x_{4} = 0 \end{cases} \\ {\begin{cases} (a_{22} - λ) x_{2} + a_{23} x_{3} + a_{24} x_{4} = - a_{21} x_{1} \\ a_{32} x_{2} + (a_{33} - λ) x_{3} + a_{34} x_{4} = - a_{31} x_{1} \\ a_{42} x_{2} + a_{43} x_{3} + (a_{44} - λ) x_{4} = - a_{41} x_{1} \end{cases} \\ [\begin{matrix} (a_{22} - λ) & a_{23} & a_{24} \\ a_{32} & (a_{33} - λ) & a_{34} \\ a_{42} & a_{43} & (a_{44} - λ) \end{matrix}] [\begin{matrix} x_{2} \\ x_{3} \\ x_{4} \end{matrix}] = [\begin{matrix} - a_{21} x_{1} \\ - a_{31} x_{1} \\ - a_{41} x_{1} \end{matrix}] \end{array}

\begin{array}{l} {\begin{cases} a_{21} x_{1} + (a_{22} - λ) x_{2} + a_{23} x_{3} + a_{24} x_{4} = 0 \\ a_{31} x_{1} + a_{32} x_{2} + (a_{33} - λ) x_{3} + a_{34} x_{4} = 0 \\ a_{41} x_{1} + a_{42} x_{2} + a_{43} x_{3} + (a_{44} - λ) x_{4} = 0 \end{cases} \\ {\begin{cases} (a_{22} - λ) x_{2} + a_{23} x_{3} + a_{24} x_{4} = - a_{21} x_{1} \\ a_{32} x_{2} + (a_{33} - λ) x_{3} + a_{34} x_{4} = - a_{31} x_{1} \\ a_{42} x_{2} + a_{43} x_{3} + (a_{44} - λ) x_{4} = - a_{41} x_{1} \end{cases} \\ [\begin{matrix} (a_{22} - λ) & a_{23} & a_{24} \\ a_{32} & (a_{33} - λ) & a_{34} \\ a_{42} & a_{43} & (a_{44} - λ) \end{matrix}] [\begin{matrix} x_{2} \\ x_{3} \\ x_{4} \end{matrix}] = [\begin{matrix} - a_{21} x_{1} \\ - a_{31} x_{1} \\ - a_{41} x_{1} \end{matrix}] \end{array}

Una onda estacionaria en una cuerda fija en sus cabos o, más concretamente, una función propia de la transformación correspondiente al transcurso del tiempo. A medida que varía el tiempo, la onda estacionaria varía en amplitud, pero su período no se modifica. En este caso el valor propio es dependiente del tiempo.

Ejemplos ;valores y vectores propios:https://www.youtube.com/watch?v=8MiOTd7cv2I

Multiplicidad algebraica y geométrica: definicion (multiplicidad algebraica). Sean V un espacio vectorial de dimensión finita, T ∈ L(V ), λ ∈ sp(T). La multiplicidad algebraica de λ se define como la multiplicidad de la raíz λ del polinomio característico CT , esto es, como max k ∈ {1, . . . , n}: (x − λ) k divide a CT .

Definición (multiplicidad geométrica). Sean V un espacio vectorial de dimensión finita, T ∈ L(V ), λ ∈ sp(T). La multiplicidad geométrica de λ se define como dim ST,λ .

Teorema (relacion entre la multiplicidad algebraica y la multiplicidad geométrica de un valor propio). Sea V un espacio vectorial de dimension finita, sea T ∈ L(V ) y sea λ ∈ sp(T). Entonces la multiplicidad geom´etrica de λ es menor o igual a la multiplicidad algebraica de λ.

Demostracion. Pongamos W = ker(λI −T), U : W → W, U(x) = T(x). Entonces U(x) = λx y por eso

CU (x) = (x − λ) k , donde k = dim(W) es la multiplicidad geometrica de λ. Sabemos que CU divide CT . Por lo tanto, la multiplicidad de la ra´ız λ del polinomio CT es mayor o igual a k.

Propiedades

Supongamos que A es una matriz de orden m. Se verifican las siguientes propiedades:

Si {v₁, . . . , v_k} son autovectores de A correspondientes a autovalores distintos λ₁, . . . , λ_k, entonces {v1, . . . , vk} son linealmente independientes.

Sean λ₁, . . . , λ_k autovalores de A distintos dos a dos. Supongamos que {v_1,1, . . . , v_1,i1} son autovectores linealmente independientes asociados a λ₁,...,{v_k,1, . . . , v_k,ik} son autovectores linealmente independientes asociados a λ_k: Entonces el conjunto formado por todos ellos

{v_1,1, . . . , v_1,i1 , . . . , v_k,1, . . . , v_k,ik}

es linealmente independiente.

Matrices semejantes y diagonalización: Dos matrices cuadradas de orden n, A y B, son semejantes si existe una matriz cuadrada, P, con determinante distinto de cero, que satisfaga B=P-1AP. A la matriz B se le llama transformada de A mediante la matriz de paso P. Propiedades:

- 1. Si A y B son semejantes , entonces son equivalentes.

- 2. Si A y B son semejantes, tienen el mismo rango.

- 3. Si (A,B) y (C, D) son semejantes con la misma matriz de paso, entonces A+C es semejante a B+D con matriz de paso P.

- 4. Si A y B son semejantes con matriz de paso P, y n es un número natural, An y Bn son semejantes con matriz de paso P.

Una matriz A es diagonalizable si es semejante a una matriz diagonal, D, es decir, si existe P regular tal que A=PDP-1 . El proceso de cálculo de la matriz diagonal y de la matriz de paso se denomina diagonalización de A.

Diagonalización de una matriz cualquiera : Sea A una matriz asociada a un endomorfismo f, definido en un espacio vectorial de dimensión n. Para diagonalizar una matriz A, tratamos de encontrar una matriz diagonal, D, semejante a la matriz A. Necesitamos encontrar una matriz de transformación o cambio de base P, que mediante la relación de semejanza P-1AP de lugar a la matriz D. Por lo tanto tenemos que encontrar una base en la que el endomorfismo quede asociado a una matriz diagonal. En algunos casos podremos encontrarlo, entonces la matriz será diagonalizable , y en otros no, no será diagonalizable.

Teorema : La condición necesaria y suficiente para que una matriz cuadrada sea diagonalizable es que exista una base del espacio vectorial formada por vectores propios del endomorfismo asociado a la matriz dada.

Matrices simétricas : Tiene especial interés la diagonalización de matrices simétricas. Supongamos que tenemos una matriz cuadrada real A de orden n que es simétrica (recordemos que esto significa que A = At ). Vamos a considerar el espacio vectorial euclídeo Rn, en el que se considera el producto escalar euclídeo. Entonces:

1. A es siempre diagonalizable sobre R, en particular sus valores propios son todos reales (no hay valores propios imaginarios).

2. Vectores propios de la matriz asociados a distintos valores propios son ortogonales.

3. Puede encontrarse una base ortogonal (e incluso ortonormal) de Rn formada por vectores propios de la matriz.

Recordemos que una matriz cuadrada A se dice que es ortogonal cuando es invertible y A−1 = At . En referencia a esto se tiene que una matriz cuadrada es ortogonal si y sólo si sus vectores-fila (o sus vectores—columna) forman una base ortonormal de espacio Rn, para el producto escalar euclídeo, y que la matriz cambio de base entre dos bases ortonormales (según el producto escalar euclídeo) es siempre una matriz ortogonal.

Sea A una matriz cuadrada real simétrica. Según lo anterior A es diagonalizable y podemos encontrar una base ortonormal B de Rn (respecto al producto escalar euclídeo) formada por vectores propios de la matriz (esto se hará escogiendo en cada subespacio propio una base ortonormal y uniendo dichas bases). Entonces en la descomposición A = PDP −1 de A, donde P = MB→C , siendo C la base canónica, se tiene que P es una matriz ortogonal, ya que es la matriz cambio de base entre dos bases ortonormales, B y C, con lo que P −1 = Pt . En esto consiste lo que denominaremos la diagonalización ortogonal de la matriz real simétrica A, en hacer la diagonalización mediante una matriz de paso ortogonal.

Diagonalización ortogonal: una matriz diremos que es ortogonal si su traspuesta coincide con su inversa.

$\begin{displaymath}P\mbox{ ortogonal }\iff P^{-1}=P^t\end{displaymath}$

Si $P=(u_1\vert u_2\vert\cdots \vert u_n)$ resulta que decir que

es ortogonal, es equivalente a decir que los vectores $\{u_1,u_2,\cdots ,u_n\}$ son ortonormales (respecto al producto escalar habitual) Para las matrices reales y simétricas podemos dar una diagonalización donde la matriz de paso es ortogonal. Esto es lo que se entiende por diagonalización ortogonal.

Sea A una matriz de orden n, entonces son equivalentes:

a) A es diagonalizable ortogonalmente.

b) A tiene un conjunto de n vectores propios ortonormales.

En álgebra lineal, una matriz cuadrada "A" se dice que es diagonalizable si es semejante a una matriz diagonal. Es decir, si mediante un cambio de base puede reducirse a una forma diagonal. En este caso, la matriz podrá descomponerse de la forma

A = PDP^{-1}

. En donde "P" es una matriz invertible cuyos vectores columna son vectores propios de A, y D es una matriz diagonal formada por los valores propios de A.

Si la matriz A es semejante ortogonalmente a una matriz diagonal, es decir, si la matriz P es ortogonal se dice entonces que la matriz A es diagonalizable ortogonalmente, pudiendo escribirse como

A = PDP^{t}

. El teorema espectral garantiza que cualquier matriz cuadrada simétrica con coeficientes reales es ortogonalmente diagonalizable. En este caso P está formada por una base ortonormal de vectores propios de la matriz siendo los valores propios reales. La matriz P es por tanto ortogonal y los vectores filas de

P^{-1}

son los vectores columnas de P.

Sea

\mathbf{A} \in M^{n \times n}(\mathbb{K})

una matriz cuadrada con valores en un cuerpo

\mathbb{K}

, se dice que la matriz

A

es diagonalizable si, y sólo si, A se puede descomponer de la forma:

$\mathbf{A} = \mathbf{P D P}^{-1}$

Donde:

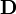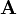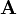$\mathbf{D}$ es una matriz diagonal cuya diagonal principal está formada por los elementos de $\sigma(\mathbf{A})$ , apareciendo cada uno tantas veces como indique su multiplicidad algebraica, siendo $\sigma(\mathbf{A})$ el espectro de $\mathbf{A}$ , es decir, el conjunto de autovalores de la matriz $\mathbf{A}$ :

$\sigma(\mathbf{A}) = \big\{ \lambda_i \in \mathbb{K}| \mathbf{Av} = \lambda_i \mathbf{v} \quad \forall i = 1,2,...,n \big\}$

$\mathbf{P}$ es la matriz cuyas columnas son los vectores que constituyen una base del subespacio propio asociado a cada $\lambda_i\,$ siguiendo el orden establecido en D, esto es, los vectores que forman el núcleo de la matriz $(A - \lambda_i I)$ :

$\mathbf{P} = (v_1 | v_2 | ... | v_n ), \quad v_j \in \mbox{ker}(\mathbf{A} - \lambda_i \mathbf{I}) \forall i,j = 1,...,n$

Diagonalización ortogonal : https://www.youtube.com/watch?v=PrmzcUTju9Y

Cónicas y superficies cuadricas : Se denomina sección cónica (o simplemente cónica) a todas las curvas resultantes de las diferentes intersecciones entre un cono y un plano; si dicho plano no pasa por el vértice, se obtienen las cónicas propiamente dichas. Se clasifican en cuatro tipos: elipse, parábola,hipérbola y circunferencia.}

En función de la relación existente entre el ángulo de conicidad (α) y la inclinación del plano respecto del eje del cono (β), pueden obtenerse diferentes secciones cónicas, a saber:

β > α : Hipérbola (naranja)
β = α : Parábola (azulado)
β < α : Elipse (verde)
β = 90º: Circunferencia (un caso particular de elipse) (rojo)

Y β= 180º : Triangular

Si el plano pasa por el vértice del cono, se puede comprobar que:

Cuando β > α la intersección es un único punto (el vértice).
Cuando β = α la intersección es una recta generatriz del cono (el plano será tangente al cono).
Cuando β < α la intersección vendrá dada por dos rectas que se cortan en el vértice.
cuando β = 90º El ángulo formado por las rectas irá aumentando a medida β disminuye,cuando el plano contenga al eje del cono (β = 0).

Partiendo de una circunferencia (e=0), al aumentar la excentricidad se obtienen elipses, parábolas e hipérbolas.

Una cuádrica es el lugar geométrico de los puntos del espacio (x,y,z) que verifican una ecuación de segundo grado del tipo

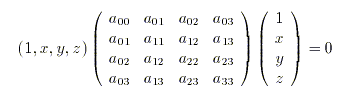
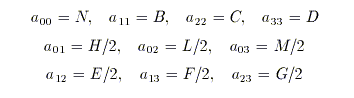
La ecuación de una cuádrica se puede escribir en forma matricial como

Denotaremos por

la matriz que define la cuádrica y por A₀₀ la matriz adjunta del elemento a₀₀ en A.

Las cuádricas se clasifican de acuerdo a su signatura s, es decir, el módulo de la diferencia entre el número de autovalores positivos y negativos de A₀₀. Sin embargo, para calcular la signatura de la cuádrica no es necesario diagonalizar la matriz, debido a la existencia de unas cantidades invariantes asociadas a A₀₀ que permiten determinar s sin necesidad de calcular explícitamente sus autovalores. Veámoslo:
los autovalores son las raíces del polinomio característico, es decir, las soluciones de la ecuación

. Ahora bien,

con

Cuando los tres autovalores de A₀₀ son no nulos, es decir, det A₀₀¹ 0, si escribimos la sucesión K, J, I, 1 y denotamos por P y V el número de permanencias y variaciones de signo que hay en ella, respectivamente, entonces |P-V| = s. Los valores I, J, K se conocen como invariantes de la cuádrica. De esta forma se tiene:

Si s = 3 :

det A > 0 ---> elipsoide real
det A < 0 ---> elipsoide imaginario (no existen puntos reales que verifican la ecuación)
det A = 0 ---> cono imaginario

Si s = 1 :

det A > 0 ---> hiperboloide hiperbólico (de una hoja)
det A < 0 ---> hiperboloide elíptico (de dos hojas)
det A = 0 ---> cono real

Si alguno de los autovalores es nulo (det A₀₀ = 0) pero el determinante de A es distinto de cero, entonces;

Si J > 0 ---> paraboloide elíptico
Si J < 0 ---> paraboloide hiperbólico

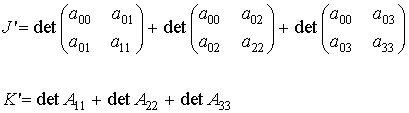
Si det A = det A₀₀ = 0, hay que introducir nuevos invariantes para completar la clasificación

donde A_ii representa la matriz adjunta del elemento a_ii en A para i=1,2,3.
Con estos nuevos invariantes se tiene

J > 0

K' ¹ 0 y signo K' = signo I ---> cilindro elíptico imaginario
K' ¹ 0 y signo K' ¹ signo I ---> cilindro elíptico real
K' = 0 ---> par de planos imaginarios secantes

J < 0

K' ¹ 0 ----> cilindro hiperbólico
K' = 0 ----> par de planos reales secantes

J = 0 y I ¹ 0

K' ¹ 0 ----> cilindro parabólico
K' = 0 y J' > 0 -- --> par de planos imaginarios paralelos distintos
K' = 0 y J' < 0 -----> par de planos reales paralelos distintos
K' = 0 y J' = 0 ----> par de planos coincidentes

En la tabla siguiente se resume la clasificación anterior:

Clasificación de las Cuádricas

det A₀₀ ¹0

s = 3

det A > 0 Elipsoide Real

det A < 0 Elipsoide Imaginario

det A = 0 Cono Imaginario

s = 1

det A > 0 Hiperboloide Hiperbólico

det A < 0 Hiperboloide Elíptico

det A = 0 Cono Real

det A₀₀ = 0

det A¹0

J > 0 Paraboloide Elíptico

J < 0 Paraboloide Hiperbólico

det A = 0

J > 0

K'¹ 0 , signo K' = signo I Cilindro elíptico imaginario

K' ¹ 0 , signo K' ¹ signo I Cilindro elíptico real

K' = 0 Par de planos imaginarios secantes

J < 0

K' ¹ 0 Cilindro hiperbólico

K' = 0 Par de planos reales secantes

J = 0 I ¹ 0

K' ¹ 0 Cilindro Parabólico

K' = 0, J' > 0 Par de planos imaginarios paralelos distintos

K' = 0, J' < 0 Par de planos reales paralelos distintos

K' = 0, J' = 0 Par de planos coincidentes

cónicas y cuadricas: https://www.youtube.com/watch?v=iX3ofAjGGjo

Álgebra lineal

viernes, 29 de abril de 2016

VALORES CARACTERÍSTICOS, VECTORES

CARACTERÍSTICOS Y FORMAS CANÓNICAS

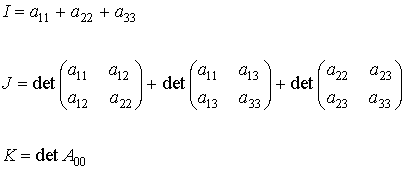
No hay comentarios:

Publicar un comentario